Research highlights : : Multiscale Modeling of Granular Media

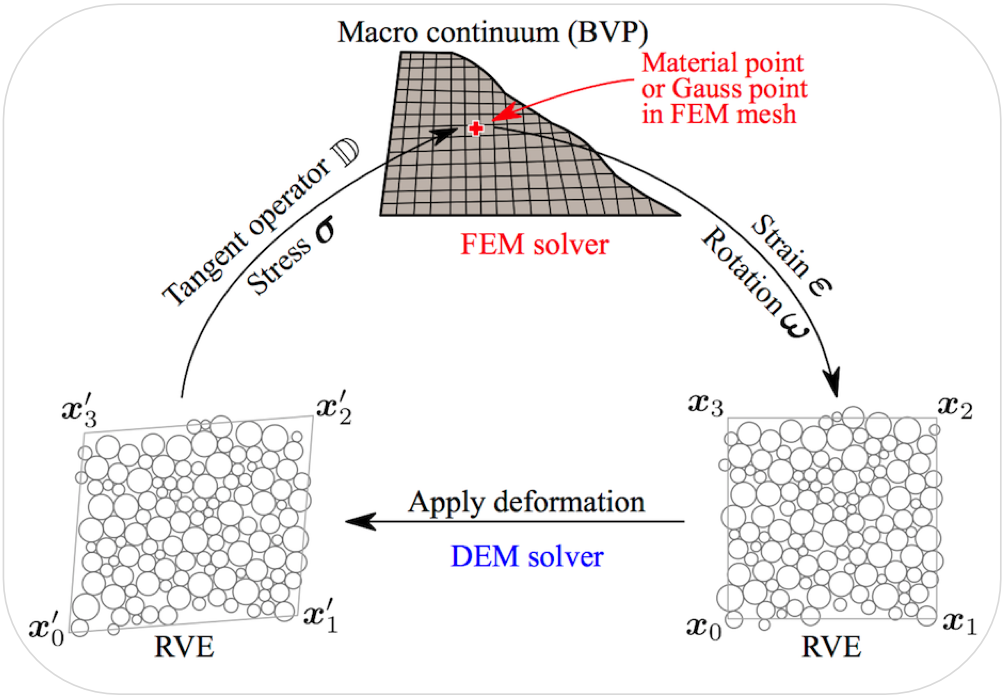
multiscale modeling for granular media (If you cannot view the SVG image properly, you are probably using a very old version of brower. Please change a newer/other browser and try again.)
Fig. 1 Schemetic illustration of the hierarchical computational framework for multiscale modeling of granular material .

Overview: Macro-Micro Bridging

A hierarchical computational multiscale framework based on rigorous coupling between the finite element method (FEM) and the discrete element method (DEM) has been developed in our Lab. As shown in Fig. 1, to solve a boundary value problem, the macroscopic geometric domain is first discretized into a FEM mesh. A DEM assembly is then embedded at each Gauss integration point of the mesh serving as a local Representative Volume Element (RVE). At each load step, the RVE takes its memory of the past loading history as initial conditions and receives the global deformation from the FEM at the specific Gauss point as input boundary conditions. It is solved to derive the local incremental stress-strain relation (e.g., stress and tangential stiffness matrix) required for advancing the global FEM computation.


Calibration of RVE
Fig.2 Calibrated RVE comprised of 400 polydisperse spheres with periodic boundary produces isotropic contact normal distribution under isotropic compression.

Calibration of RVE

To calibrate the size of the RVE (e.g., particle number), different RVEs with different particle numbers subject to isotropic compression have been compared and the resultant contact normal distribution is examined. A typical RVE containing 400 particles (for 2D) and with periodic boundary is found to provide largely isotropic contact normal distribution and meanwhile offer reasonable computational efficiency (see Fig 2).This number may be tripled if a three-dimensional problem is to be tackled.


biaxial shear of dense sand
Fig.3 Multiscale modeling of monotonic biaxial shear of dense sand: (left) model setup; (right) global stress strain relation.

Biaxial Shear of Medium Dense Sand

We applied the multiscale appraoch to predicting the sand response subject to monotonic biaxial shear (see the FEM model setup in Fig. 3, left). The global stress strain response measured from the boundary reaction forces and displacements are compared against the the pure DEM simulaiton on a RVE size sample in Fig. 3(right). The two are in reasonable agreement with each other. Notably the post-peak response of the DEM test shows moderate fluctuations, while the multiscale results are relatively smooth.


localisation in biaxial shear
Fig.4 Localized strain and void ratio in sand sample subject to biaxial shear (a) at peak stress (b) at final state.

Strain localization in Biaxial Shear

The occurrence of strain localisation commonly found in laboratory biaxial shear tests on sand was captured by our multiscale simulation (see fig. 4). For a homogeneous sample under smooth and symmetric boundary conditions, strain localization is observed in our multiscale simulation, which otherwise cannot be observed by conventional continuum modeling approaches (they commonly need to introduce imperfactions or random field for material parameters to trigger strain localization in this case). Our study found the direct trigger is the non-coaxial local material response due to very mild initial anisotropy, and it actually incepts d prior to the peak. At final state, the void ratio is found localized in slightly wider zone than the accumulated deviatoric strain.


microstructures in biaxial shear
Fig. 5 Internal structure of force chain network of the local initial and deformed RVE and the corresponding fabric anisotropy.

Microstructures in Biaxial Shear

A major advantage of the multiscale framework is the rich microscale inforamtion it can provide and link directly to the simulated macroscopic behavior. Fig. 5 shows a comparison of the contact force network for RVE packings at three Gauss points, illustrating severe shear deformation for Gauss point within the shear band (No. 256), mild shear deformation for point outside the band (No. 51), as well as the failed point due to volumetric expansion at the shear band boundary (No. 422).




References: